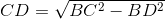Contoh Soal dan Pembahasan Segitiga Secara Lengkap

Contoh Soal dan Pembahasan Segitiga Secara Lengkap
Contoh soal 1:
Perhatikan gambar berikut!

Tentukan nilai x dan besar sudut A pada segitiga diatas !

Pembahasan:
180º = ∠A+∠B+∠C
180º = (3x + 10°) + (x + 15°) + 35°
180º = 4x + 60°
4x=180°-60°
4x = 120°
x = 120°/4
x = 30°

Besar ∠A = 3x + 10°

∠A = 3(30°) + 10°

∠A = 90° + 10° = 100°

Contoh soal 2:

Perhatikan gambar berikut!

Tentukan luas dari:

a. ΔACD

b. ΔBCD

c. ΔABD

Pembahasan:

ΔACD: Perhatikan gambar dibawah, daerah yang berwarna kuning adalah segitiga ACD

Berdasarkan gambar diketahui:

Panjang alasnya = AC = 4 cm

Tingginya = AD = 10 cm

L ΔACD = ½ × AC × AD

L ΔACD = ½ × 4 × 10

L ΔACD = 20 cm²

b. ΔBCD : Daerah yang berwarna biru pada gambar diatas adalah segitiga BCD

Berdasarkan gambar diketahui:

Panjang alasnya = BC = 4 cm

Tingginya = AD = 10 cm (tingginya tetap AD, karena tinggi segitiga adalah garis yang tegak lurus dengan alasnya)

L ΔBCD = ½ × BC × AD

L ΔBCD = ½ × 8 × 10

L ΔBCD = 40 cm²

c. ΔABD : Daerah yang berwarna hijau pada gambar dibawah adalah segitiga ABD

Berdasarkan gambar diketahui:

Panjang alasnya = AB = 8 + 4 = 12 cm

Tingginya = AD = 10 cm

L ΔBCD = ½ × AB × AD

L ΔBCD = ½ × 12 × 10

L ΔBCD = 60 cm²

Contoh soal 3:

Tentukan panjang CD dan luas segitiga ABC pada gambar berikut!

Pembahasan:

a. Panjang CD: (menggunakan rumus Phytagoras)

b. Luas ΔABC

Panjang alasnya = AB = 12 cm

Tinggi = CD = 10 cm

L ΔBCD = ½ × AB × CD

L ΔBCD = ½ × 12 × 12

L ΔBCD = 72 cm²

Contoh soal 4:

Hitunglah panjang EG pada gambar berikut!

Pembahasan:

Agar dapat mengitung panjang EG terlebih dahulu kita harus mengetahui panjang EF.

Panjang EF pada ΔDEF dapat dicari dengan teorema Phytagoras:

Contoh soal 4:

Hitunglah panjang EG pada gambar berikut!

Pembahasan:

Agar dapat mengitung panjang EG terlebih dahulu kita harus mengetahui panjang EF.

Panjang EF pada ΔDEF dapat dicari dengan teorema Phytagoras:

Panjang EG pada ΔEFG:

Contoh soal 5:

Sebuah segitiga sama kaki mempunyai keliling 98 cm, jika panjang alasnya 24 cm, hitung luas segitiga tersebut!

Pembahasan:

Diketahui:

Panjang alas = 24 cm

keliling = 98 cm

keliling = sisi1 + sisi2 + alas

98 cm = sisi1 + sisi2 + 24 cm

Sisi1 + sisi2 = 98 – 24 = 74 cm (ingat, dalam segitiga sama kaki sisi1 = sisi2)

Maka sisi 1 = sisi 2 = 74/2 = 37 cm.

Untuk mencari luas segitiga, kita harus mengetahui tinggi dari segitiga tersebut. Tinggi segitiga dapat dicari menggunakan rumus Phytagoras (dengan sisi 1 atau sisi 2 sebagai sisi miring (37 cm), dan alasnya yaitu ½ alas segitiga tersebut (24/2 = 12 cm))